搜索与图论
dfs
排列数字
给定一个整数 n,将数字 1∼n排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤7
输入样例:
输出样例:
code
#include <iostream>
using namespace std;
const int N = 10;
int path[N];
bool st[N];
int n;
void dfs(int u) {
if (u == n) {
for (int i = 0; i < n; i++) cout << path[i] << ' ';
puts("");
}
for (int i = 1; i <= n; i++) {
if (!st[i]) {
st[i] = true;
path[u] = i;
dfs(u + 1);
st[i] = false;
}
}
}
int main() {
cin >> n;
dfs(0);
return 0;
}
n-皇后问题
n−n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 nn,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
输出样例:
code
2^(n^2)
每个点都需要访问俩次
#include <iostream>
using namespace std;
const int N = 13;
char g[N][N];
int n;
bool row[N], col[N], dg[2 * N], udg[2 * N];
void dfs(int x, int y, int s) {
if (y == n) {
x++, y = 0;
}
if (x == n) {
if (s == n) {
for (int i = 0; i < n; i++) cout << g[i] << endl;
puts("");
}
return;
}
if (!row[x] && !col[y] && !dg[y - x + n] && !udg[y + x]) {
row[x] = col[y] = dg[y - x + n] = udg[y + x] = true;
g[x][y] = 'Q';
dfs(x, y + 1, s + 1);
row[x] = col[y] = dg[y - x + n] = udg[y + x] = false;
g[x][y] = '.';
}
dfs(x, y + 1, s);
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) g[i][j] = '.';
}
dfs(0, 0, 0);
return 0;
}
o(n^2)
#include <iostream>
using namespace std;
const int N = 13;
char g[N][N];
bool col[N], dg[2 * N], udg[2 * N];
int n;
void dfs(int u) {
if (u == n) {
for (int i = 0; i < n; i++) {
cout << g[i];
puts("");
}
puts("");
return;
}
for (int i = 0; i < n; i++) {
if (!col[i] && !dg[i - u + n] && !udg[u + i]) {
col[i] = dg[i - u + n] = udg[u + i] = true;
g[u][i] = 'Q';
dfs(u + 1);
col[i] = dg[i - u + n] = udg[u + i] = false;
g[u][i] = '.';
}
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) g[i][j] = '.';
dfs(0);
return 0;
}
bfs
走迷宫
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m) 处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
输出样例:
code
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int g[N][N], d[N][N];
int n, m;
void bfs() {
queue<PII> q;
memset(d, -1, sizeof d);
d[0][0] = 0;
q.push({0, 0});
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while (!q.empty()) {
auto t = q.front();
q.pop();
for (int i = 0; i < 4; i++) {
int x = t.first + dx[i], y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) {
d[x][y] = d[t.first][t.second] + 1;
q.push({x, y});
}
}
}
cout << d[n - 1][m - 1];
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) cin >> g[i][j];
}
bfs();
return 0;
}
八数码
在一个 3×33×3 的网格中,1∼81∼8 这 88 个数字和一个 x 恰好不重不漏地分布在这 3×33×3 的网格中。
例如:
在游戏过程中,可以把 x 与其上、下、左、右四个方向之一的数字交换(如果存在)。
我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
例如,示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。
交换过程如下:
现在,给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
输入格式
输入占一行,将 3×33×3 的初始网格描绘出来。
例如,如果初始网格如下所示:
则输入为:1 2 3 x 4 6 7 5 8
输出格式
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出 −1−1。
输入样例:
输出样例
code
#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>
using namespace std;
int bfs(string start) {
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0 , -1};
string end = "12345678x";
queue<string> q;
q.push(start);
unordered_map<string, int> dist;
dist[start] = 0;
while (!q.empty()) {
auto t = q.front();
q.pop();
int distance = dist[t];
if (t == end) return distance;
int k = t.find('x');
int x = k / 3, y = k % 3;
for (int i = 0; i < 4; i++) {
int a = x + dx[i], b = y + dy[i];
if (a >= 0 && a < 3 && b >= 0 && b < 3) {
swap(t[k], t[a * 3 + b]);
if (!dist[t]) {
dist[t] = distance + 1;
q.push(t);
}
swap(t[k], t[a * 3 + b]);
}
}
}
return -1;
}
int main() {
string start = "";
for (int i = 0; i < 9; i++) {
char c;
cin >> c;
start += c;
}
cout << bfs(start);
return 0;
}
图的深度优先遍历
树的重心
给定一颗树,树中包含 n 个结点(编号 1∼n)和 n−1 条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数 n,表示树的结点数。
接下来 n−1 行,每行包含两个整数 a 和 b,表示点 a 和点 b 之间存在一条边。
输出格式
输出一个整数 m,表示将重心删除后,剩余各个连通块中点数的最大值。
数据范围
1≤n≤10^5
输入样例
输出样例:
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], idx;
bool st[N];
int ans = N, n;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dfs(int u) {
int sum = 1, res = 0;
st[u] = true;
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) {
int s = dfs(j);
res = max(res, s);
sum += s;
}
}
res = max(res, n - sum);
ans = min(ans, res);
return sum;
}
int main() {
cin >> n;
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i++) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
dfs(1);
cout << ans;
return 0;
}
图的广度优先遍历
图中点的层次
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 1,点的编号为 1∼n。
请你求出 1 号点到 n 号点的最短距离,如果从 1 号点无法走到 n号点,输出 −1。
输入格式
第一行包含两个整数 n 和 m。
接下来 mm 行,每行包含两个整数 a 和 b,表示存在一条从 a 走到 b 的长度为 1 的边。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
数据范围
1≤n,m≤10^5
输入样例:
输出样例:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int d[N], hh, tt, q[N], n, m;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int bfs() {
memset(d, -1, sizeof d);
q[0] = 1;
d[1] = 0;
while (hh <= tt) {
auto t = q[hh++];
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] == -1) {
d[j] = d[t] + 1;
q[++tt] = j;
}
}
}
return d[n];
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b);
}
cout << bfs();
return 0;
}
n皇后
截距
1111
图:
1.邻间矩阵
二维数组
2.邻间表
很多个单链表
e :值
h 头
ne next
idx 边
ans = answer res = result vis = visited dx, dy 方向向量 stk = stack q = queue dummy 链表虚拟头节点
st state
有向图才有拓扑序列
有向无环图:拓扑图
1->2
1->3
2->3
1 2 3
起点在终点前面
1
入度 有几点边指向他 0
出度 有几点边指出去 2
有向图的拓扑序列
给定一个 n 个点 m 条边的有向图,点的编号是 1 到 n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1。
若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 x 和 y,表示存在一条从点 x 到点 y 的有向边 (x,y)。
输出格式
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出 −1。
数据范围
1≤n,m≤10^5
输入样例:
输出样例:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int q[N], hh, tt = -1, d[N], n, m;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool tup_sort() {
for (int i = 1; i <= n; i++) {
if (!d[i]) q[++tt] = i;
}
while (hh <= tt) {
auto t = q[hh++];
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
d[j]--;
if (!d[j]) q[++tt] = j;
}
}
return tt == n - 1;
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b), d[b]++;
}
if (tup_sort()) {
for (int i = 0; i < n; i++) printf("%d ", q[i]);
} else cout << -1;
return 0;
}
最短路
最短路
1单源最短路 一个点到其他所有点的最短路
1.1
n:点的数量 m 边的数量
所有边权都是正数(朴素Dijkstra算法 n*n 稠密图、堆优化版的Dijkstra算法 mlogn )
1.2
存在负权边 (Bellman-Ford nm, SPFA m 最坏 nm)
2多源汇最短路: 起点 终点 不确定
Floyd n^3
稠密图 领接矩阵
朴素dijkstra-Dijkstra求最短路 I
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z 表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n≤500, 1≤m≤10^5, 图中涉及边长均不超过10000。
输入样例:
输出样例:
o(n^2 + m)
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int g[N][N], d[N], n, m;
bool st[N];
int dijkstra() {
memset(d, 0x3f, sizeof d);
d[1] = 0;
for (int i = 0; i < n; i++) {
int t = -1;
for (int j = 1; j <= n; j++) {
if (!st[j] && (t == -1 || d[j] < d[t])) t = j;
}
st[t] = true;
for (int j = 1; j <= n; j++) d[j] = min(d[j], d[t] + g[t][j]);
}
if (d[n] == INF) return -1;
return d[n];
}
int main() {
cin >> n >> m;
int a, b, w;
memset(g, 0x3f, sizeof g);
while (m--) {
scanf("%d%d%d", &a, &b, &w);
g[a][b] = min(g[a][b], w);
}
cout << dijkstra();
return 0;
}
堆优化-Dijkstra求最短路 II
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n,m≤1.5×1e5, 图中涉及边长均不小于 0,且不超过 10000。 数据保证:如果最短路存在,则最短路的长度不超过 1e9。
输入样例:
输出样例:
mlogn
#include <bits/stdc++.h>
using namespace std;
const int N = 150010, INF = 0x3f3f3f3f;
typedef pair<int, int> PII;
int h[N], e[N], ne[N], w[N], idx, d[N], n, m;
bool st[N];
void add(int a, int b, int c) {
w[idx] = c, e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dijkstra() {
memset(d, 0x3f, sizeof d);
priority_queue<PII, vector<PII>, greater<PII>> q;
q.push({0, 1});
d[1] = 0;
while (!q.empty()) {
auto t = q.top();
q.pop();
int distance = t.first, ver = t.second;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (distance + w[i] < d[j]) {
d[j] = distance + w[i];
q.push({d[j], j});
}
}
}
if (d[n] == INF) return -1;
return d[n];
}
int main() {
cin >> n >> m;
int a, b, c;
memset(h, -1, sizeof h);
while (m--) {
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
cout << dijkstra();
return 0;
}
Bellman-ford 算法-有边数限制的最短路
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离,如果无法从 1 号点走到 n 号点,输出 impossible。
注意:图中可能 存在负权回路 。
输入格式
第一行包含三个整数 n,m,k。
接下来 m 行,每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。
如果不存在满足条件的路径,则输出 impossible。
数据范围
1≤n,k≤500, 1≤m≤10000, 任意边长的绝对值不超过 10000。
输入样例:
输出样例:
bellman_ford
**o(nm) **
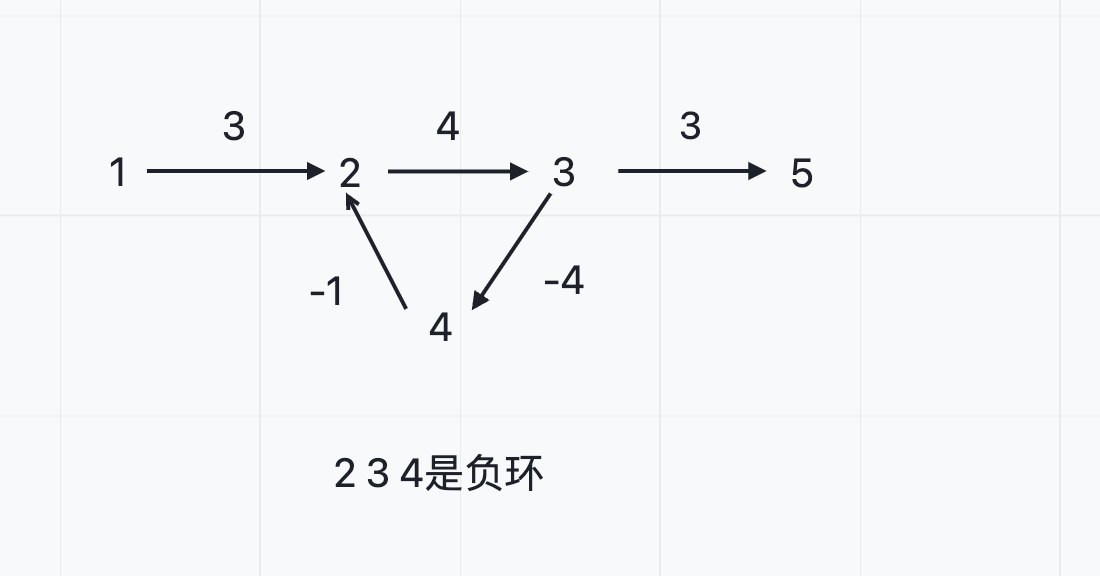
允许有负权边
经过1条边最短
经过2条边最短
....
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 510, M = 1e5 + 10;
struct Edge {
int a, b, w;
} e[M];
int dist[N], back[N];
int n, m, k;
void bellman_ford() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < k; i++) {
memcpy(back, dist, sizeof dist);
for (int j = 0; j < m; j++) {
int a = e[j].a, b = e[j].b, w = e[j].w;
dist[b] = min(dist[b], back[a] + w);
}
}
if (dist[n] > 0x3f3f3f / 2) puts("impossible");
else printf("%d", dist[n]);
}
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 0; i < m; i++) {
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
e[i] = {a, b, w};
}
bellman_ford();
return 0;
}

dijkstra 不能负边
为了避免如下的串联情况, 在边数限制为一条的情况下,节点3的距离应该是3,但是由于串联情况,利用本轮更新的节点2更新了节点3的距离,所以现在节点3的距离是2。
1 2 1
2 3 1
1 3 3
Bellman-Ford:不能有负环
spfa 最短路 -> bellman_ford的队列优化
给定一个 nn 个点 mm 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出 11 号点到 nn 号点的最短距离,如果无法从 11 号点走到 nn 号点,则输出 impossible。
数据保证不存在负权回路。
输入格式
第一行包含整数 nn 和 mm。
接下来 mm 行每行包含三个整数 x,y,zx,y,z,表示存在一条从点 xx 到点 yy 的有向边,边长为 zz。
输出格式
输出一个整数,表示 11 号点到 nn 号点的最短距离。
如果路径不存在,则输出 impossible。
数据范围
1≤n,m≤1051≤n,m≤105, 图中涉及边长绝对值均不超过 10000
输入样例:
输出样例:
st:是否在队列中
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], w[N], idx, n, m, d[N];
bool st[N];
void add(int a, int b, int c) {
w[idx] = c, e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void spfa() {
memset(d, 0x3f, sizeof d);
queue<int> q;
q.push(1);
d[1] = 0;
st[1] = true;
while (q.size()) {
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[t] + w[i] < d[j]) {
d[j] = d[t] + w[i];
if (!st[j]) {
st[j] = true;
q.push(j);
}
}
}
}
if (d[n] == 0x3f3f3f3f) puts("impossible");
else cout << d[n];
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
int a, b, c;
while (m--) {
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
spfa();
return 0;
}
3f3f3f3f
最小生成树
1普利姆算法prim
稠密 朴素 n^2
稀疏 堆优化 mlogn
2克鲁斯卡尔算法 Kruskal
稀疏
mlogm
二分图
染色法
n + m
匈牙利算法
最坏 mn 一般远小于o(mn)
最小生成树:n个城市建公路 最短
二分图:当且仅当图中不奇数环(环有奇数条边)
二分图:集合集合之间有边 集合内部没有边
算法导论:算法证明
prim算法:更新每个值
先更新后面就不会更新了
最小生成树
一个连通图可能有多个生成树。当图中的边具有权值时,总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和
Prim算法求最小生成树
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w表示点 u和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
1≤n≤500, 1≤m≤10^5, 图中涉及边的边权的绝对值均不超过 10000。
输入样例:
输出样例:
code
o(n*n + m)
稠密图
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int g[N][N], dist[N], n, m, a, b, w;
bool st[N];
int prim() {
int res = 0;
memset(dist, 0x3f, sizeof dist);
for (int i = 0; i < n; i++) {
int t = -1;
// 找到距离集合最近的一个且没有访问过的点
for (int j = 1; j <= n; j++) {
if (!st[j] && (t == -1 || dist[j] < dist[t])) t = j;
}
if (i && dist[t] == INF) return INF;
if (i) res += dist[t];
st[t] = true;
// a -> b -> c c是b的基础来的, 所以需要更新值
// 为下次找最近的点做准备:更新所有点到集合的距离
for (int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) if (i != j) g[i][j] = INF;
}
while (m--) {
cin >> a >> b >> w;
g[a][b] = g[b][a] = min(g[a][b], w);
}
int res = prim();
if (res == INF) puts("impossible");
else cout << res;
return 0;
}
st[t] = true;
Kruskal算法求最小生成树
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 EE 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
1≤n≤1e5, 1≤m≤2∗1e5, 图中涉及边的边权的绝对值均不超过 1000。
输入样例:
输出样例:
code
mlogm
稀疏图
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 2 * N, INF = 0x3f3f3f3f;
struct Edge {
int a, b, w;
bool operator<(const Edge &E) const {
return w < E.w;
}
}e[M];
int n, m, p[N];
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kurskal() {
int cnt = 0, res = 0;
for (int i = 0; i < m; i++) {
int a = e[i].a, b = e[i].b, w = e[i].w;
if (find(a) != find(b)) {
p[find(a)] = p[find(b)];
cnt++;
res += w;
}
}
if (cnt < n - 1) return INF;
return res;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) p[i] = i;
int a, b, c;
for (int i = 0; i < m; i++) {
cin >> a >> b >> c;
e[i] = {a, b, c};
}
sort(e, e + m);
int res = kurskal();
if (res == INF) puts("impossible");
else cout << res;
return 0;
}
m
for (int i = 0; i < m; i++) { cin >> a >> b >> c; e[i] = {a, b, c}; }
if (find(a) != find(b)) {
二分图
染色法判定二分图
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环。
请你判断这个图是否是二分图。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示点 u 和点 v 之间存在一条边。
输出格式
如果给定图是二分图,则输出 Yes,否则输出 No。
数据范围
1≤n,m≤10^5
输入样例:
输出样例:
code
i - j
i j属于不同的集合
o(n+m)
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], idx;
int color[N], n, m;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u, int c) {
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!color[j] && !dfs(j, 3 - c)) return false;
else if (color[j] == c) return false;
}
return true;
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
while (m--) {
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
bool flag = true;
for (int i = 1; i <= n; i++) {
if (!color[i] && !dfs(i, 1)) {
flag = false;
break;
}
}
if (!flag) puts("No");
else puts("Yes");
return 0;
}
二分图最大匹配
给定一个二分图,其中左半部包含 n1 个点(编号 1∼n1),右半部包含 n2 个点(编号 1∼n2),二分图共包含 m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
二分图的匹配:给定一个二分图 G,在 G 的一个子图 M 中,M 的边集 {E}中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
输入格式
第一行包含三个整数 n1、 n2 和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示左半部点集中的点 u 和右半部点集中的点 v 之间存在一条边。
输出格式
输出一个整数,表示二分图的最大匹配数。
数据范围
1≤n1,n2≤500, 1≤u≤n1, 1≤v≤n2, 1≤m≤10^5
输入样例:
输出样例:
code
o(nm)
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 510, M = 1e5 + 10;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];
int n1, n2, m;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int u) {
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) {
st[j] = true;
if (match[j] == 0 || find(match[j])) {
match[j] = u;
return true;
}
}
}
return false;
}
int main() {
cin >> n1 >> n2 >> m;
memset(h, -1, sizeof h);
while (m--) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
}
int res = 0;
for (int i = 1; i <= n1; i++) {
memset(st, false, sizeof st);
if (find(i)) res++;
}
cout << res;
return 0;
}
if (!match[j] || find(match[j]))
match[j]放弃
test
1
bfs1: n m
bfs2 unordered_map
2
bellman_ford:
忘记初始化d
3
prim:
st[t] = true
kruskal:
for (int i = 0; i <m ;i ++)
3.4
if (match[j] || find(match[j])) {}